Der Widerstandsguide
Wenn du mit Elektronik arbeitest, wirst du über kurz oder lang nicht an Widerständen vorbeikommen. Es ist nicht gut, wenn an I/O Pins über einen längeren Zeitraum eine höhere Spannung anliegt oder hoher Strom fließt. Das kann auch die Bauteile beschädigen. Mit Widerständen können wir diesem Problem entgegenwirken. Doch auch wenn in der Anleitung bestimmte Widerstände angegeben werden, müssen diese erstmal erkannt werden. Dafür gibt es ein universelles System mit Farbringen, mit dem der Wert eines Widerstands mit ein wenig Geduld abgelesen werden kann.
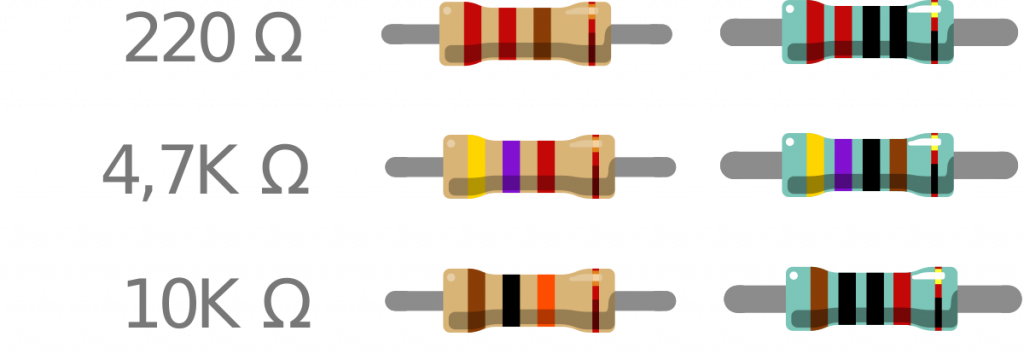
Generell wird beim Ablesen zwischen den Widerständen mit vier und fünf Ringen unterschieden.
Beispiel 1

Gut, gehen wir ein Beispiel nochmal zusammen durch. Insgesamt gibt es 4 Ringe. Also schauen wir uns die Tabelle für die Widerstände mit vier Ringen an. Der erste Ring ist braun, also 1. Der zweite Ring ist schwarz, das ist eine 0. Insgesamt haben wir also 10. Der dritte Ring ist orange, das bedeutet, dass der Multiplikator 1000 ist. Folglich beträgt der Widerstandswert 10 * 1000 = 10 000. Weil es immer nervig ist, so große Zahlen aufzuschreiben, können wir 1000 auch mit k abkürzen, in unserem Fall wäre das also 10kΩ. (Das k steht dabei für Kilo, was aus dem altgriechischen kommt und Eintausend bedeutet. Vermutlich kennst du das schon von anderen Einheiten wie zum Beispiel: kg oder km. Der vierte Ring sagt etwas über die Toleranz aus. Die Toleranz liegt bei ±5%. Das heißt, in unserem Beispiel liegt der tatsächliche Widerstandswert zwischen 9 500Ω und 10 500Ω. Wenn es also zu 110% ein 10kΩ sein muss, müssen wir auch dementsprechend einen Widerstand nutzen, der diesen Toleranzbereich hat. Bei unseren Schaltungen spielt das aber keine Rolle.
Beispiel 2

Und damit du nicht aus der Übung kommst, machen wir noch ein zweites Beispiel zusammen. Insgesamt gibt es 5 Ringe. Also müssen wir uns die Tabelle mit den fünf Ringen ansehen. Der erste Ring ist rot, also 2. Der zweite Ring ist auch rot, auch eine 2. Der dritte Ring ist schwarz, also eine 0. Insgesamt haben wir also 220. Der dritte Ring ist schwarz, das heißt, der Multiplikator ist 1. Der Widerstandswert beträgt somit 220 * 1 = 220 . Mit dem fünften Ring können wir noch die Toleranz herausfinden. Die Toleranz liegt bei ±1%. Das heißt der tatsächliche Widerstandswert liegt zwischen 219 Ω und 225 Ω..
Vier Ringe
| Farbe | 1. Ring (Zehner) | 2. Ring (Einer) | 3. Ring (Multiplikator) | 4. Ring (Toleranz) |
| silber | – | – | 0,01 | ±10 % |
| gold | – | – | 0,1 | ±5 % |
| schwarz | – | 0 | 1 | – |
| braun | 1 | 1 | 10 | ±1 % |
| rot | 2 | 2 | 100 | ±2 % |
| orange | 3 | 3 | 1 000 | – |
| gelb | 4 | 4 | 10 000 | – |
| grün | 5 | 5 | 100 000 | ±0,5 % |
| blau | 6 | 6 | 1 000 000 | ±0,25 % |
| violett | 7 | 7 | 10 000 000 | ±0,1 % |
| grau | 8 | 8 | 100 000 000 | ±0,05 % |
| weiß | 9 | 9 | 1 000 000 000 | – |
Fünf Ringe
| Farbe | 1. Ring (Hunderter) | 2. Ring (Zehner) | 3. Ring (Einer) | 4. Ring (Multiplikator) | 5. Ring (Toleranz) |
| silber | – | – | 0,01 | – | |
| gold | – | – | – | 0,1 | – |
| schwarz | – | 0 | 0 | 1 | – |
| braun | 1 | 1 | 1 | 10 | ±1 % |
| rot | 2 | 2 | 2 | 100 | ±2 % |
| orange | 3 | 3 | 3 | 1 000 | – |
| gelb | 4 | 4 | 4 | 10 000 | – |
| grün | 5 | 5 | 5 | 100 000 | ±0,5 % |
| blau | 6 | 6 | 6 | 1 000 000 | ±0,25 % |
| violett | 7 | 7 | 7 | ±0,1 % | |
| grau | 8 | 8 | 8 | ±0,05 % | |
| weiß | 9 | 9 | 9 | – |
